Каковы примеры системы типов объектов, подобных локальному калибровочному преобразованию и напряженности поля?

Question

Каковы примеры системы типов объектов, подобных локальному калибровочному преобразованию и напряженности поля?

Николай-К

По сути, это продолжение, мотивированное этим ответом на мой вопрос об интерпретации калибровочных преобразований типов идентичности.

Поле

ψ : М \to С^{н}

$\psi:\mathcal M\to\mathbb C^n$ является частью

C^{n}

$\mathbb C^n$ -расслоение над пространственно-временным многообразием

M

$\mathcal M$ . Имеем локальные калибровочные преобразования

ψ (Икс) \mapsto ψ^{'} (Икс) "=" U (Икс) ψ (Икс) : (М \to С^{н}) \to (М \to С^{н}) .

$\psi(x)\mapsto \psi'(x):=U(x)\,\psi(x)\ :\ (\mathcal M\to \mathbb C^n)\to(\mathcal M\to \mathbb C^n).$

Теперь рассмотрим язык с полиморфизмом типов и класс $M$ всех его типов, элементы которых могут быть помещены в список. Позволять $\Psi$ — полиморфная функция, которая для каждого типа $X\in M$ , отображает $X$ -list в целое число, а именно его длину. Например, используя синтаксис Haskell , если $X=\mathrm{Bool}$ , затем $\Psi_\mathrm{Bool}\left([\mathrm{True},\mathrm{True},\mathrm{False}]\right) = 3$ . В обозначениях системы F мы имеем

Ψ : \forall Икс . ([Икс] \to я н т) .

$\Psi:\forall X.\left([X]\to\mathrm{Int}\right).$

Калибровочные преобразования должны соответствовать отображениям

ты : \forall Икс . ([Икс] \to я н т) ⟶ \forall Икс . ([Икс] \to я н т) .

$u\ :\ \forall X.\left([X]\to\mathrm{Int}\right)\ \longrightarrow\ \forall X.\left([X]\to\mathrm{Int}\right).$

я мог бы придумать некоторые $u$ , например, сопоставление функции длины $\Psi$ к карте $\Psi':=u\,\Psi$ который вместо этого возвращает в 42 раза больше длины списка. Но это было бы, с точки зрения физики, глобальным калибровочным преобразованием, потому что оно не чувствительно к типу $X$ . Я думаю, учитывая, что единственным инвариантом конечномерного векторного пространства является его мощность, в этом случае не должно быть возможности построить локальное преобразование. Что может быть практическим примером локального калибровочного преобразования в этом смысле?

Более того, я хотел нарисовать повседневную жизнь параллельно типам личности. Ну, во-первых, есть небольшое препятствие, заключающееся в том, что приведенное выше преобразование не может быть задано выражением в большинстве языков, поскольку типы обычно не являются объектами первого класса. Я предполагаю, что этот выбор дизайна сделан потому, что в противном случае вывод типа был бы испорчен. В теории гомотопических типов у вас есть реализация того, что «типы тоже являются терминами» (через n-категории?), И тогда это возможно. Но в любом случае я все еще не могу точно определить спецификацию, когда тип является идентификационным типом. Я понимаю «тождество» для гомотопически эквивалентных пространств и калибровочно-инвариантных лагранжианов, но существуют ли негеометрические структуры, в частности релевантные для программирования,

редактировать : я сделал две визуализации примера здесь и потом:

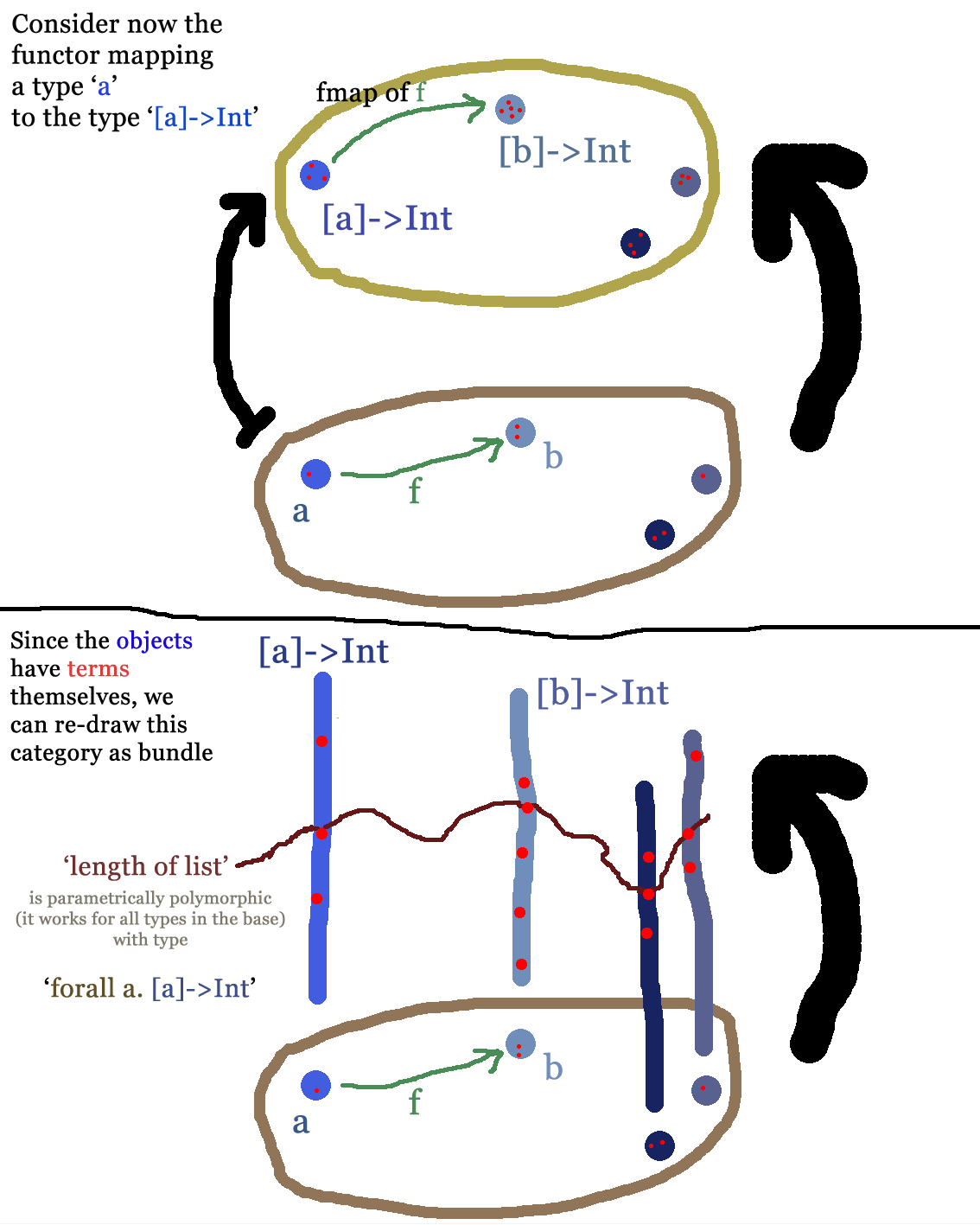
введите описание изображения здесь

Тогда возникает вопрос, какой будет разумная мера сечения на втором рисунке. (Я также сделал еще две картинки, выходящие за рамки того, что просили: естественные преобразования и монады, как в Haskell .)

Кстати, я знаю, что HoTT реализует зависимые типы , а не «просто» параметрически полиморфные, но это не должно быть препятствием.

Ответы (1)

Каковы примеры системы типов объектов, подобных локальному калибровочному преобразованию и напряженности поля?

Урс Шрайбер · Answer 1

В этом вопросе затрагивается множество самых разных аспектов. Я постараюсь дать некоторые указания. Но я замечаю, что связь этого вопроса с реальной физикой не очень сильна, вместо этого вопрос кажется более общим после того, как я получил представление о типах идентичности в теории гомотопических типов (HoTT). Я предполагаю, что есть другие дискуссионные группы, более подходящие для такого рода вопросов, например, группа Google с (возможно, неудачным) названием « Любители HoTT », в которую вы могли бы подумать о размещении вопросов.

Теперь по вопросам, кратко пробежавшись сверху вниз:

во-первых, карта $\mathcal{M} \to \mathbb{C}^n$ это $\mathbb{C}^n$ -значная функция на $\mathcal{M}$ . Можно рассматривать это как часть $\mathbb{C}^n$ -пучок волокон над $\mathcal{M}$ , да, но тогда это будет тривиальное такое расслоение волокон.

(Секции нетривиальных пакетов могут быть закодированы в HoTT с использованием зависимых типов. Если вы действительно хотите узнать больше об этом, дайте мне знать, и я расширю).

Затем по поводу автоэквивалентностей типа функций из списков в натуральные числа: действительно, я полагаю, что у этого не будет много автоэквивалентностей. Если бы мы рассматривали не натуральные числа, а целые числа, то были бы некоторые очевидные (а именно, добавить +1 к каждой функции, обратной которой была бы операция, добавляющая -1).

Затем, что касается вопроса о том, как идентифицировать тип идентичности: нельзя смотреть на произвольный тип и спрашивать: «Это тип идентичности?» (Можно сделать это, но я не думаю, что это то, что вам нужно.) Скорее, для данного типа создается соответствующий тип идентичности. (Заметьте также, что тип идентичности некоторого типа $X$ является $X \times X$ -зависимый тип. )

Учитывая вышеприведенные вопросы, мне кажется, что в центре внимания находятся не столько реальные приложения к физике, сколько получение базового представления о теории гомотопических типов как таковой. Для этой цели я полагаю, что нет ничего лучше, чем проработать книгу HoTT . (Полагаю, вы это уже знаете, но все же позвольте мне еще раз подчеркнуть.)

Спасибо за ответ. 1) Добавление $\pm 1$ снова глобальный, поскольку он не видит типы, но теперь я это понимаю. 2) Я хочу понять, почему датчики следует рассматривать как типы идентичности. Вы сказали: «Примечательно, что когда теория гомотопических типов снабжена дополнительной аксиомой дифференциальной связности, тогда можно «дифференцировать» типы идентичности». Есть ли что-то, что мы получаем от HoTT, чего у нас нет, если мы, даже более непосредственно, создадим подходящий топос для нашей физики? Т.е. есть ли причина, по которой типы на самом деле являются здесь преимуществом, кроме того мета-преимущества, что сейчас им интересуется множество разных людей?
Отвечая на ваш вопрос: да, в HoTT есть калибровочные преобразования, которых нет в обычном топосе. Например, в связном HoTT есть тип BU(1)_conn электромагнитных калибровочных полей. Этого нет ни в одном простом топосе (1-топосе). Для многообразия X функция X --> BU(1)_conn является электромагнитным калибровочным полем на X, а гомотопия между двумя такими отображениями является калибровочным преобразованием между конфигурациями этих полей. Этот аспект калибровочной/гомотопической теории отсутствует в обычном топосе.

Каковы примеры системы типов объектов, подобных локальному калибровочному преобразованию и напряженности поля?

Николай-К

Ответы (1)

Урс Шрайбер

Николай-К

Урс Шрайбер

Как физик воспринимает калибровочные поля

Интерпретируются ли типы идентичности физически в бесконечно-топосной формулировке уравнений движения?

Происхождение интеграла от тензора напряженности поля в линейной экспоненте в калибровочной теории поля

Является ли подключение манометра уникальным?

Операции над формами со значениями алгебры Ли на главном расслоении

Диффеоморфизмы, изометрии и общая теория относительности

Что для физика инстантоны и инварианты Дональдсона?

7 сфера, есть ли физическая интерпретация экзотических сфер?

Калибровочные поля и строки: уравнения цикла

Почему в электромагнетизме только калибровочные преобразования?